多次元時系列分析ツールを公開しました
先日我々の論文がPhilosophical Transactions of the Royal Society Aから出版されました。
この論文はEnergy Landscape Analysis [1-3] という分析手法についてまとめた論文です。それに合わせて今回、誰でも(MATLABさえあれば)簡単にこの手法が使えるようにプログラムを公開しましたのでこの機会に詳しく書いてみたいと思います。
何ができる分析なのか?
多次元の時系列(例えば脳の様々な領域からとってきた活動データなど)を(単に個々の活動の総和としてではなく)全体として分析したほうが本質的なことがわかる場合があります。しかし、多次元の時系列は状態空間の次元が高く、何がどうなっているか理解するためには何らかの方法で低い次元での動きに読み直してやる必要があります。
これを解決する方法の一つがEnergy Landscape Analysis [1-3] です。この手法ではデータから尤もらしいモデル分布を推定し、それを元にして状態空間をエネルギー地形に見立てて粗視化することができます。
尚、脳のfMRIデータを例としていますが、(基本的には)多次元の時系列であればなんのデータにでも使えます。
手法の詳細

この分析では、まず2値化した(活動が高い=+1,低い=–1とした)時系列を考えます。
一つの領域(変数)ごとに+1/–1で2パターンあるので、N個の領域を分析すると2^N個の活動パターンが発生しえます。データの中でそれぞれのパターンが何回現れたかをカウントすることで出現の確率分布を得ることができます。
次に、この確率分布をボルツマン分布でfittingします。Maximum Entropy Distributionとも言います。また、統計物理の文脈ではIsing(スピングラス)模型の定常確率分布です。このfittingですが、時系列の一次と二次のモーメント(=平均と相関)はデータとモデルでぴったり一致させることができます。ただ、Nが大きくなると厳密にこれを求めるのは現実的ではなくなり、近似手法に頼ることになります。ちなみに、三次以降の項は無視して大丈夫なのかというと、少なくともfMRIのデータでは(今のところ)大体よさそうです。
このモデル分布は式の定義の中に「エネルギー」が入っていて、フィッティングができた時点でそれぞれの活動パターンにひとつずつエネルギーの値が割り振られたことになります。
エネルギーが低い状態は出現頻度が高く、したがって重要な状態である可能性が高いです。そこで、それらの状態がエネルギー的にどのような位置関係になっているかを分析するとdisconnectivity graphと呼ばれるデンドログラムが書けます。
また、エネルギーの谷底(local minimum)になっているところの周り(basin)にどのような状態が集まっているのかも決定することができます。
こうして、すべての2^N個の状態にエネルギーの谷底(local minimum)かその周囲(basin)のラベルが付きます。すると、元の時系列が今そのEnergy Landscapeの中でどこにいるのかを定義することができ、このエネルギー地形を状態が動いていくという解釈をすることが可能となります。
公開したプログラム(Energy Landscape Analysis Toolkit: ELAT)
ダウンロードはこちらから
今回、この分析を簡単に利用してもらえるように時系列データを読み込むだけで全部自動的に出してくれるMATLABのプログラムコードを公開しました。ここではその使い方とできることについて紹介したいと思います。
準備
1.分析する時系列データを用意してください。現状、変数の数は20以下くらいでないとうまく分析できません。ファイルは数字だけからなるデータで各行が各変数の時系列になるようにします。つまり横(列)方向に時間が進んでいく向きで準備してください。連続値のデータの場合はELATが指定された閾値で二値化しますが、それが嫌な場合(データによってはもっと良い方法があるはずなので)はご自分で二値化した後のデータを準備します。
2.変数名リストのファイルを用意していただけると出力結果に反映されます。なくても動きます。
3.私のサイトからELATをダウンロードしていただき、適当なところに解凍してください。
ELATの使い方
1.MATLABを起動し、”StartProgram.m”を実行します。すると次のようなウィンドウが出ます。
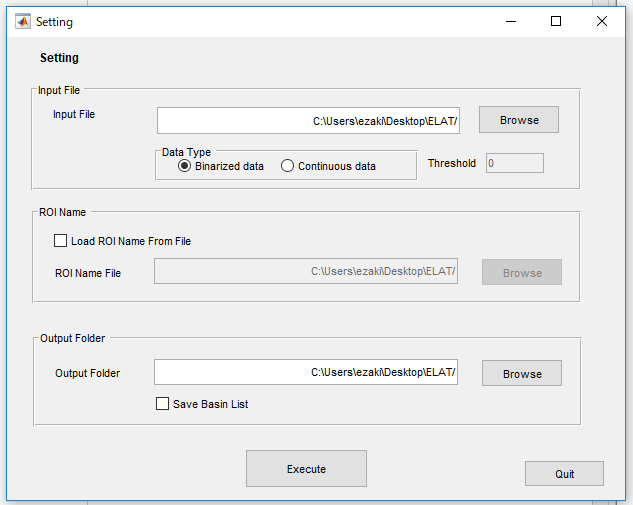
2.データファイルを読み込みます。テストデータとして"testdata.data"が入っているのでとりあえず動くか試してみたい方はそれを読み込んでください。
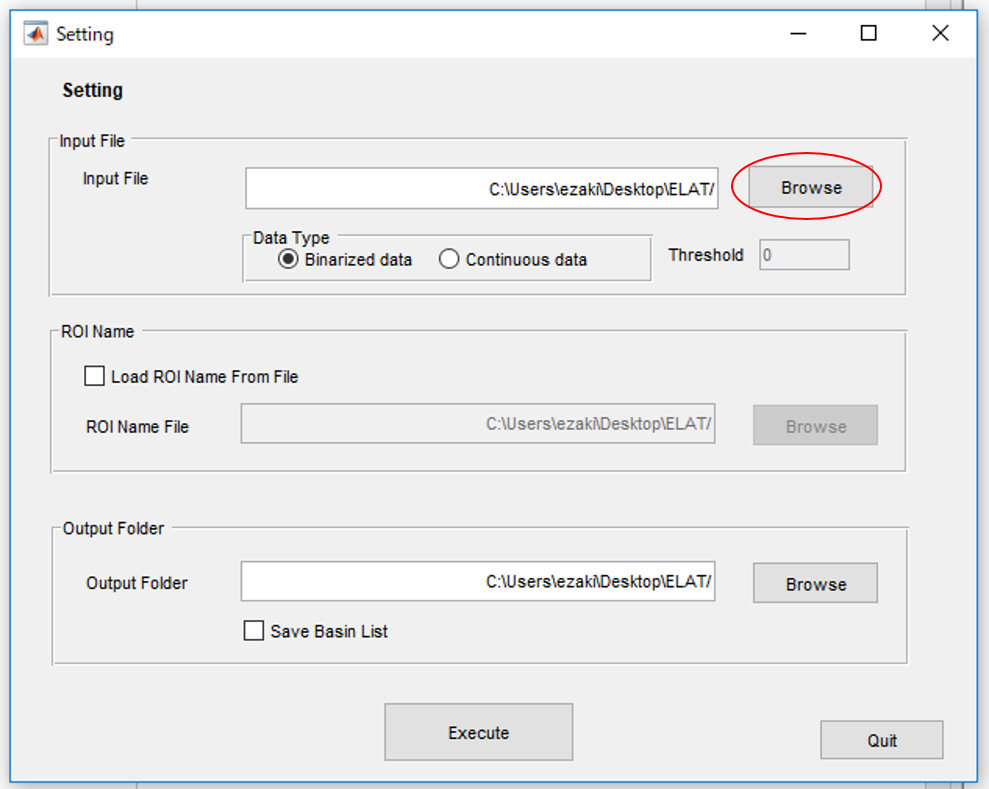
3.テストデータは既に二値化されているのでData typeは"Binarized data"を選択します。
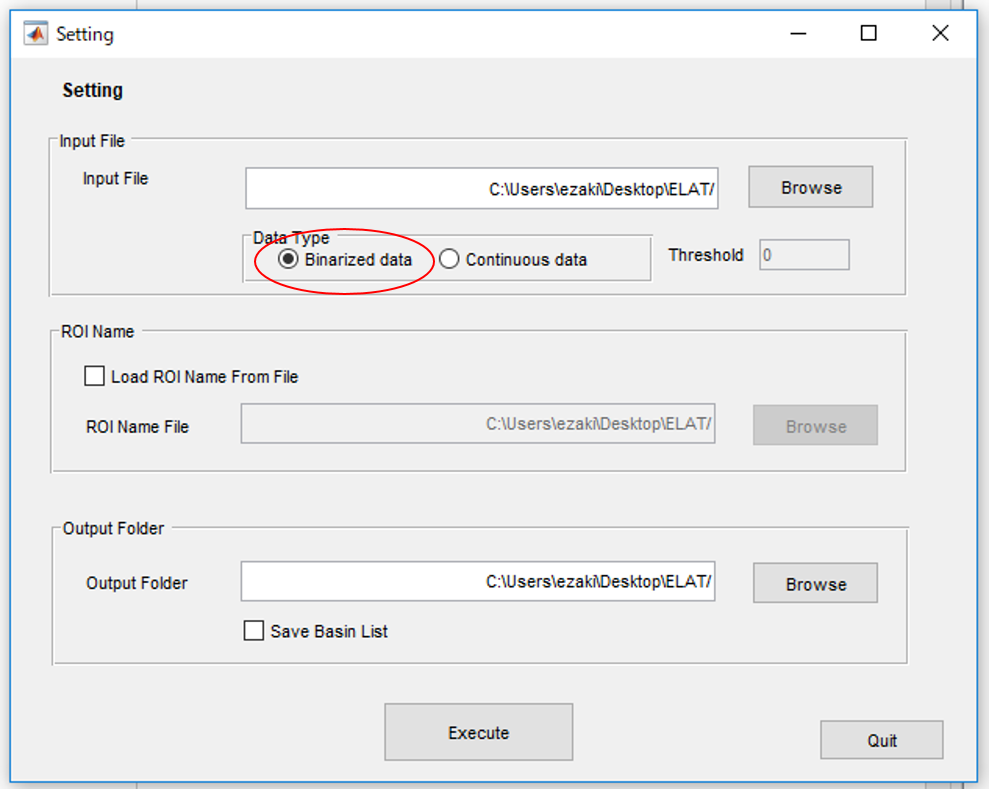
連続値のデータを読み込んだ場合は、"Continuous data"の方を選択します。この時Thresholdが選択できますが、特段の理由がなければデフォルトの0のままで良いと思います。尚、fMRIデータでgroup内の被験者をひとまとめにpoolしたデータの場合、二値化は被験者ごとにやったほうが良い(base lineの値が違ったらこまる)ので、先に別途二値化したものを用意することをお勧めします。
4.変数名(ここでは、脳の領域の名前)のリストが(あれば)読み込みます。ここではテストデータ"roiname.dat"を読み込みます。
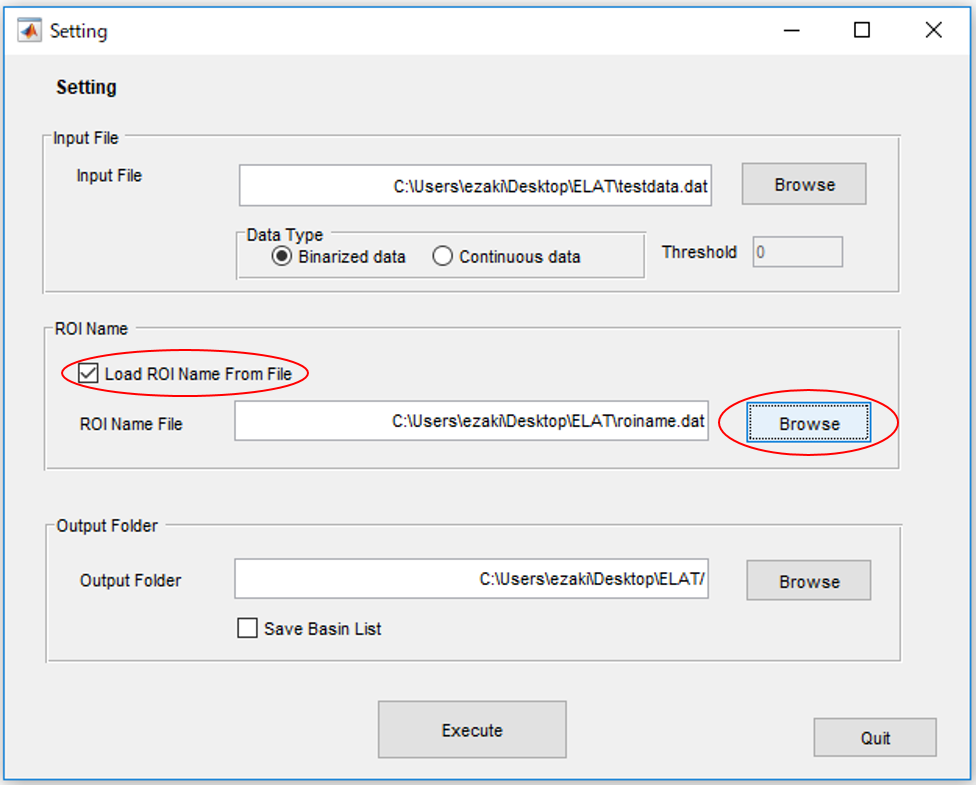
5.最後に結果が保存されるフォルダを指定します。後の分析のためにbasinの定義(どの状態がどのエネルギーの谷に属するか)も保存したい場合は"Save Basin List"にチェックを入れます。
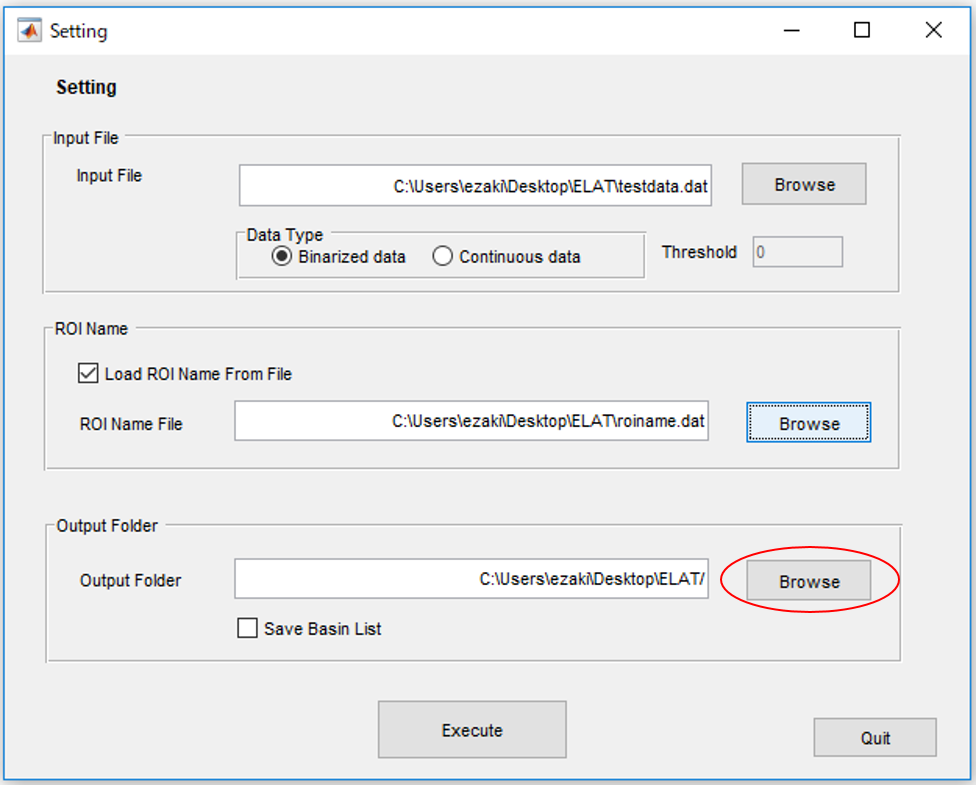
6.Executeを押します。
結果
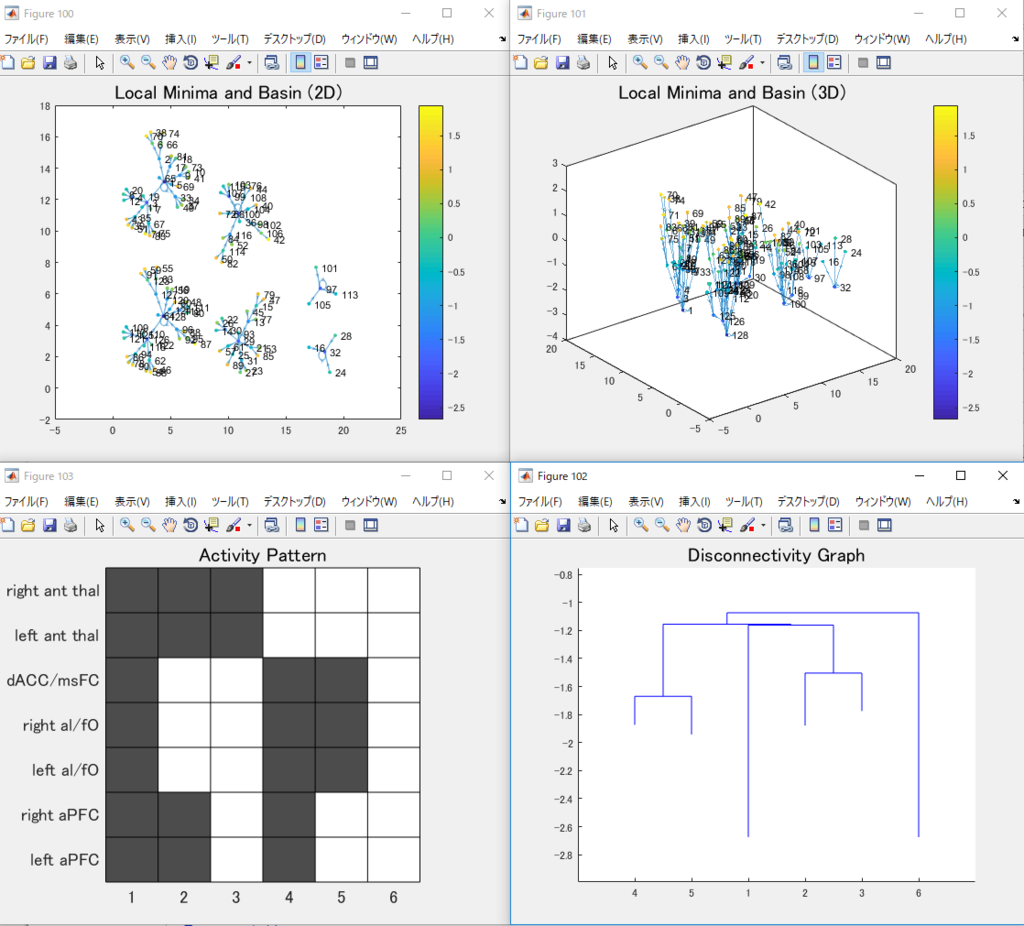
上段の二枚は2^N個の状態をlocal minimumとそのbasinに分類した絵です。
数字はそれを二進数表示にして、1 → +1, 0 → –1と読み替えたときに出てくるパターンに対応します。色と高さはエネルギーの値を表します。
下段の右はdisconnectivity graphでlocal minimumになっている状態の間をエネルギー地形の上で行き来するときにどれだけエネルギー差があるかをまとめたものです。横軸は状態(定義は下段左)で縦軸はエネルギーの値を表します。
この後は何をすればいいのか?
この分析では、状態空間を粗視化したものとエネルギー地形的な解釈を与えますが、それだけで分析が終了ということではなく、それを足掛かりにしてより詳細な分析を行います。問題の対象や設定によって異なると思いますが、例えば
1.disconnectivity graphの形が条件AとBで異なっているかをみる
2.あるlocal minimumの周りでの状態の滞在時間や遷移レートなどの指標に着目してデータを分析する
などが考えられます(具体例については論文 [1] のイントロで紹介した文献をご参照ください)。
その他注意事項
1.このコードを実行するためにはMATLABの2016bよりも新しいバージョンおよび Statistics and Machine Learning Toolboxが必要です。
2.時系列の変数の数ですが15より小さいくらいでないと動きません。ただ、ボルツマン分布を求める部分については数百まで増やしても動きます(が、データによってパフォーマンスはまちまちなようです)。
3.同梱されているmain.mで一通りの分析が行えますので、適宜ご利用ください。
4.理論的なことや技術の詳細に関しては論文 [1](OAなので誰でも読めます)に書いてありますのでご参照ください。
5.バグや質問等ありましたら江崎でご連絡ください。
[1] T. Ezaki, T. Watanabe, M. Ohzeki, and N. Masuda, "Energy landscape analysis of neuroimaging data", Phil. Trans. R. Soc. A 375, 20160287 (2017).
[2] T. Watanabe, N. Masuda, F. Megumi, R. Kanai, G. Rees, "Energy Landscape and dynamics of brain activity during human bistable perception", Nat. Commun. 5, 4765 (2014).
[3] T. Watanabe, S. Hirose, H. Wada, Y. Imai, T. Machida, I Shirouzu, Y. Miyashita, N. Masuda, "Energy Landscapes of resting-state brain networks", Front. Neuroinform. 8, 12 (2014).