Stanford滞在記2、3週間目~日常
あっという間に時間が過ぎるようになってきた
前回の更新がちょうど一週間たったところだったので、間が二週間ほど空いたことになります。この二週間の間は大して新しい発見やイベントがあったというわけでもなく、生活が日常と化してきたというところです。こうなってくると毎日のsurpriseがないからか時間があっという間に過ぎるようになるみたいです。
日々の生活
ここまでところの生活は以下のような感じです。
毎日朝6~7時くらいに起きて、8時からキャンパス内のスタバに行きます。ここはどうやら朝5時半とかから空いているようで、慣れてきたらもう少し朝早く行くことにもトライしてみたいとは思っていますが、こちらは日の出が遅く、朝7時くらいまでは普通に暗いし寒いのであんまり外に出たくないなという理由でまだやっていません(特に危険というわけではないです)。そこで昼まで仕事をします。昼になると昼食を取りにくる人が増えるからかwifiがつながらなくなるのでそこで強制終了になります。。
昼は適当に食べます。キャンパスのスタバがある周辺は色々とランチボックスを売っているので買って食べるか、そんなにおなかがすいてなければリュックサックに常備してある穀物バーを食べます。
午後はラボに行きます。ラボには基本的に毎日ポスドクさんが2,3人とアシスタントさんがいて、基本的には皆静かに集中して仕事をしていますが、偶にたわいもない会話やたわいもなくない会話などで盛り上がります。そのまま6時くらいまで仕事をします。少し疲れたら近くのカフェでコーヒーなどを入手してブレイクするときもあります。みんな基本的には6時くらいで帰ります。
そのまま家に帰ります。自転車で大体10分くらいで帰れます。荷物を置いたら徒歩数分の所にあるwhole foods marketというスーパーに行き、バイキング形式で好きなものをとれる惣菜コーナーで晩御飯を入手します。従量課金制で、1ポンド1000円くらいですが、普通においしい料理が簡単に手に入るので非常に良いです。大体いつも1200円分くらいの分量を購入してそこで食べるか持って帰って部屋で食べます。
食事を終えたらシャワーを浴びます。大体これで7時過ぎくらいです。元気があればそこから11時くらいまで仕事をします。元気がなければ適当にツイッターやyoutubeなど見て過ごします。大体11時~12時に寝ます。もう少し早めに寝ることもあります。睡眠時間は長めですが、日本にいるときはあまり規則正しい生活をしていなかったのでいつもより長くなっているのかいつも通りなのかは分かりません笑 ただ、日本にいるときよりも色々と身の回りに気を張っていないといけないのでその分精神的に疲れているかもしれないな、という気もします。
英語
英語について。特に海外に住んだ経験はなかったので心配していましたが今のところ割と大丈夫です。もともと英語はそれなりには得意だったのですが、今回に先立って英語のリスニングはネットフリックスで鍛えました。google chromeのアドイン?で日本語と英語の字幕を同時に出すことができるのですが、その状態でThe Big Bang TheoryとSuitsを片っ端から観まくる(+暇な時間とか常に流しっぱなしにしておく)ことを続けていたらかなり聴き取れるようになりました。ただ、聞き取りやすい人の言っていることは大体全部わかるのですが癖のあるしゃべり方をする人の言ってることは全然わかりません。それと、気づいたことですが、英語って(あるいは言語一般に言えることかもしれませんが)単純に単語やフレーズを音で聞き取れる能力だけでなく、こういうシチュエーションだとこうフレーズ言うよねみたいな前提の統計分布を持っていることの方が重要だということが分かってきた気がします。
食事
アメリカというと食事が不健康なものしかないというイメージを持っていたのですが、それは恐らく地域によって大分異なっていて、私が今いるあたりはかなりヘルシーで美味しい食べものが沢山あります。寧ろラーメン三昧していた日本にいたときより健康な食生活になっている気がします(笑)。日本食も驚くほどまともなレベルのものが浸透していて、あまり日本食が恋しくなりません(スーパーの寿司などもOKなレベルものが多いですし、ラーメン凪などのハイクオリティな日本のラーメン屋も複数進出しています)。というわけで平均的にはヨーロッパのその辺の都市と比べて明らかに食事のレベルは高いといえると思います。また、値段は日本の感覚でいえば高いですが、ヨーロッパなどと比較して特に高いということもなく(地価・家賃は本当に高いですが)いい感じです。
そんなこんなで早くも4週間目に突入ですが、引き続き頑張っていきたいと思います。
Stanford滞在記5,6,7日目~作業環境は整ってきた
5,6日目 初めての土日
一応土日で洗濯等をする予定だったので、宿泊施設に備え付けの洗濯機・乾燥機と格闘。最終的に何とかちゃんと洗濯することはできて、滞在中の洗濯環境がとりあえず問題なさそうで安心しました。
自室で仕事できる環境(と自分がそれに慣れること)は大体準備ができてきました。コーヒーが簡単に手に入るとベストなのですが、面倒そうなので滞在中はフレーバーティーで行くことにします(数種類購入してきました)。SONYのノイズキャンセリングヘッドフォンをこちらにくる直前に購入したのですが、同じ建物に泊まってる他のゲストの生活音(洗濯機やシャワーなど)も気にせず仕事に集中できてとても良いです。

こちらに来てから初めての土日ですが、スーパーも大学のカフェも大体平日と同じように空いています。大学の中もかなり人がいます。(平日よりはサークル活動?的な集まりの人が多い印象です)

7日目 ちょうど一週間
この一週間を振り返ると大体時差ボケも直ってきて、環境も整ってきたというとこです。普通の仕事もそれなりに集中してできるようになりました(基本、自室 or スタバ)。ただ、まだいろいろと手続きが残っていて、IDカードの発行や、滞在先の研究室の建物の鍵をもらったりしなければなりません。また、研究倫理やハラスメント講習みたいなものも結構な分量でやらなければならず(かなりの量の資料を読んでクイズに答えなければならない)、立ち上げに少し時間がかかることは仕方ないと割り切って一つ一つ片付けていこうというところです。本格的な共同研究のスタートはそれからとなるのでもう少しというところでしょうか。睡眠のサイクルがこちらの時間に適応できたくらいで日々の生活をルーティン化していきたいところです。
食事に関しては色々開拓出来ていて、本日はラーメン凪のパロアルト店に行ってみたり(日本と同等のクオリティのものが出てきました。尚、煮干しラーメンではなくて、日本で豚王として展開しているとんこつラーメンの方(と多分同じもの)だけの提供です)

学内にもいくつかレストランやショップがありますが、とりあえずサブウェイの注文は無事できました。

サブウェイ(確か上記で8ドルくらい)に比べるとピザ(4ドルくらい)はコスパが良いです。

コスパといえば、スーパーで売ってる、鶏一羽まるまるローストしたもの。これがわずか10ドルで買えます。普通に二日に分けても食べ切れないくらいの量なのでうまく活用できれば良さそうです(味が薄い部分など飽きてしんどいです)。

そんなこんなで、ここ一週間は良い調子でうまく環境に慣れることができてきた気がします。明日以降も引き続き、頑張ろうと思います。
Stanford滞在記2,3,4日目~チャリがしんどい
Stanfordでの生活も少し落ち着いてきました。
二日目
前回のブログ:
でも書いた通り、キャンパスが広大で、キャンパス内移動だけでもかなり時間がかかります。というわけで自転車を買いに行くことにしました。
大学の中でも買えるのですが、結構値段が高いらしいという情報を聞きつけ、Targetという日用品量販店?で買うことにしました。

この店内にある商品、値札が付いていないものが結構あって、そういう時は店員に聞くか、店内に設置されたバーコードリーダーにかざすと値段が分かるようになっているようです。。
そして良さそうな自転車があったので購入。

値段は全部込みで3万円くらいでした。
帰りは折角買った自転車で家までサイクリングすることに。地図ではすぐ帰れそうなようにも見えるのですが、実際距離を計算すると5マイルほどあります。あんまり普段の距離感でわからないのですが、後で計算したところ私が普段使っている井の頭線で換算すると大体10駅分くらい(!)の距離だったようです。。。
google mapにも自転車の移動時間は表示されますが、これは恐らくガチ勢の人の速度でこいだ場合の話で、普通の場合×1.5倍はしないといけないということを知りました。。
あと、スマホを固定できるホルダー、非常に重宝しました。このくらいの距離の移動だと、google mapのGPS表示をすぐ見れる状況になっていないと大変な目にあいます。
あと、サドルがやけに固いので相当お尻に来ます。普段自転車に乗らないこともあって、筋肉痛もやばいです。このブログを書いている本日は一日乗らない予定なので回復するといいのですが。。
三日目
formalにはここからStanfordに通いだしました。Stanfordで対応してくれている職員の方に挨拶。色々を説明を受けて、アカウントを使えるようにしたり、机をもらったり。皆さんとてもいい人で、非常にフレンドリーに迎えていただけました。
学内の中心部にはカフェとか食堂が集まっている領域があって、スタバは作業場として使えそうです。(ほとんどの学生さん?は一人でPCで一生懸命作業しています)

4日目
今回ホストとして受け入れてくれているProf. Manish Saggarと面会。こちらも歓迎してもらい、彼のラボを案内してもらった後、今後の研究テーマに関するディスカッション。一応事前にこんなことをやろうということは決めてあるのですが、それ以外にも色々できそうだよねということでいい感じです。建物に入るために必要なIDや、CITI(研究倫理などに関する講習)を完了させる必要があるので、すぐスタートというわけにはいかないようですが、来週から動き出せるのではないかと思っています。
夜は友人から教えてもらったイベントに参加して決ました。JTPAというこのあたりにいる日本人の技術系の人たちの集まりで、今回はFacebook AI Researchの矢井田翔さんの機械学習を物理で理解するtalkがありました。話の内容も非常に面白かったですし、その後の懇親会でも面白い方々と出会うことができました。
どうやら、私と同じようにStanfordにVisiting Scholarとして(特に企業から)来ている人は沢山いらっしゃるようだということ、日本人に限らずStanfordの内外で色々なイベント・セミナー・カンファレンスがかなりの頻度で行われているようだということで、色々勉強する機会に恵まれそうです。
とりあえず今のところ食事はそこまで不自由せず来ています(ヘルシーな食事ができているとは言えないですが。。)

今週はこんな感じで無事生活のセットアップが完了したかなというところです。あまり仕事ができていないので(このブログには記載していない時間で多少はやっているのですが)来週からはうまく研究を含めた生活のルーティン化を進めていきたいところではあります。
Stanford滞在記1日目
はじめに
本日から3か月間Visiting ScholarとしてStanford大学で研究させていただけることになりました。詳しいことや滞在に関するTipsは後でまとめて記事にしたいと思いますが、とりあえず、日々あったことを記録がてら書いていこうと思います。
既に自分も体感しているのですが、この手の情報は以外にネットで調べてもよくわからなかったりするので、しょうもない日記だったとしても将来どなたかの何かの役に立つかもしれないという意図もあります。
来る前の生活の準備について
基本的に私は海外出張は2週間とかでも最小限の荷物(普通のリュックサック1個分)で行く人間なのですが、今回は三か月ということで流石にスーツケースを買いました。
普段もっていくもの(パスポート、必要書類、髭剃り、歯ブラシ、携帯PCなど&充電器、3・4日分の服、機内で使うスリッパ・アイマスク・耳栓・ネックピロー)と比較して追加したものは、
・海外で使えるSIMカード
アメスマという会社のものを使っていますが、今のところいい感じです。使い放題で月5000円くらい。
・シャンプー、洗顔料、整髪料、洗剤
普段は現地調達でいいのですが、このあたりの違和感がジワジワストレスになったら嫌なので持ってきました。
・粉末出汁、みそ汁パック
粉末出汁はあご出汁とカツオ出汁をもってきてみました。使うかどうかはわかりません。
・服を少し多めに
一週間で洗濯するシステムです。現地で調達することも考えましたが、買いに行くのも距離的に結構面倒そうだったので持ってきました。
借りた部屋
今回、滞在する宿はAirbnbでとりました。Stanfordの近く(というか東京にいる自分の基準だとすごい距離の範囲ですが)はシリコンバレーで、どこも滅茶苦茶に家賃が高いです。(危険なエリアを除けば)
まともなワンルームの部屋だと月50万とかはざらです。今回はシェアハウス的な感じのお部屋(ただし割と隔離されている)を借りて、大学からの近さを優先することにしました。
Airbnbのレビューには「立地が最高、大学にも近くのショッピングモールにも歩いて行ける」、みたいなことが書いてあって、それは事実だったのですが、大学まで行こうと思ったら大体徒歩30分くらいはかかります(泣)。地図の縮尺が私が想定していたものと全然違くて、激近と思っていたところでこれか、、という感じでした。
しかし、逆に言うと、これ以上遠い物件にしていたら絶望感がすごかったと思うので、その点は良かったです。
部屋は綺麗で、バスルーム・キッチンは他の利用者とシェアですが、いい感じです。

サンノゼ空港~パロアルト
サンノゼ空港からパロアルトまではバスと電車で一時間くらいでいけます。サンノゼ空港に鉄道駅は恐らくないので、バスかタクシーかUberかで移動する必要があります。サンノゼ空港からは無料のバスが出ていて(VAT#10)サンタクララ駅まで行けます(ちなみに地図で見ると一見徒歩でも行けそうに見えますが、実際は1時間ほどかかりますし、道沿いにはほとんど何もないです)。ここで電車(caltrain)に乗って30分ほどです。電車の切符は駅のホームで購入することができて、操作も比較的わかりやすいので迷うことはないです。この時点で携帯のネットが使えると、こういう移動の時でもgoogle mapのルート検索が使えて便利です。

パロアルト
パロアルトには近くにショッピングモール(日本でいうとアウトレットモールみたいな雰囲気です)があります(駅から徒歩10分くらい)。ショッピングや見て回るのは楽しいですが、普段の生活に役に立ちそうなお店はあまりないです。宿のチェックインまで時間があったのでその足でスタンフォード大学に行ってみました。そこから徒歩25分くらいです。
一度ちらっと行ったことはあったのですが、この大学、敷地面積がとんでもなく広いです。
いま調べたところ、なんと約33万キロ平方メートル。これは東京でいえば杉並区と大体同じ面積らしいです。意味が分からん。。。
というわけで大学の中心の領域まで行くのにも一苦労ですが、中に入ると建物がどれも非常に綺麗でいい感じです。


食料の確保
さて、この滞在中の食事をどうするかを考えなければなりません。特に夜は、レストランは一人ではなかなか入りづらそうですし、お金もかかります。となると、出来合いのものを購入したり、自炊したりといった選択肢がありそうです。近くのスーパー(Whole Foods Market)に行ってみると、かなり色々売っていました。キッチンが充実していれば自炊もやりがいがありそうです。中でも、ビュッフェ形式で好きなものだけ好きなだけとれる販売形式の総菜(重さ1ポンド当たり10ドル)はすごく良さそうで、今日軽くやってみただけでも6ドルくらいで美味しい料理を手に入れることができました。これは時間の意味でもお金の意味でもコスパがかなりいいので、早くも毎日の晩御飯の最有力候補です。
後は大学の中の食堂もあてにしているのですがそれについては後日確かめることにしましょう。
それと、ここで無事水も確保しました。まず、初日でとりあえずサバイバルに必要な安定的な水と食料と寝床を確保することができました。

今日はこんなところでおしまいです。明日も頑張っていきたいと思います。
多次元時系列分析ツールを公開しました
先日我々の論文がPhilosophical Transactions of the Royal Society Aから出版されました。
この論文はEnergy Landscape Analysis [1-3] という分析手法についてまとめた論文です。それに合わせて今回、誰でも(MATLABさえあれば)簡単にこの手法が使えるようにプログラムを公開しましたのでこの機会に詳しく書いてみたいと思います。
何ができる分析なのか?
多次元の時系列(例えば脳の様々な領域からとってきた活動データなど)を(単に個々の活動の総和としてではなく)全体として分析したほうが本質的なことがわかる場合があります。しかし、多次元の時系列は状態空間の次元が高く、何がどうなっているか理解するためには何らかの方法で低い次元での動きに読み直してやる必要があります。
これを解決する方法の一つがEnergy Landscape Analysis [1-3] です。この手法ではデータから尤もらしいモデル分布を推定し、それを元にして状態空間をエネルギー地形に見立てて粗視化することができます。
尚、脳のfMRIデータを例としていますが、(基本的には)多次元の時系列であればなんのデータにでも使えます。
手法の詳細

この分析では、まず2値化した(活動が高い=+1,低い=–1とした)時系列を考えます。
一つの領域(変数)ごとに+1/–1で2パターンあるので、N個の領域を分析すると2^N個の活動パターンが発生しえます。データの中でそれぞれのパターンが何回現れたかをカウントすることで出現の確率分布を得ることができます。
次に、この確率分布をボルツマン分布でfittingします。Maximum Entropy Distributionとも言います。また、統計物理の文脈ではIsing(スピングラス)模型の定常確率分布です。このfittingですが、時系列の一次と二次のモーメント(=平均と相関)はデータとモデルでぴったり一致させることができます。ただ、Nが大きくなると厳密にこれを求めるのは現実的ではなくなり、近似手法に頼ることになります。ちなみに、三次以降の項は無視して大丈夫なのかというと、少なくともfMRIのデータでは(今のところ)大体よさそうです。
このモデル分布は式の定義の中に「エネルギー」が入っていて、フィッティングができた時点でそれぞれの活動パターンにひとつずつエネルギーの値が割り振られたことになります。
エネルギーが低い状態は出現頻度が高く、したがって重要な状態である可能性が高いです。そこで、それらの状態がエネルギー的にどのような位置関係になっているかを分析するとdisconnectivity graphと呼ばれるデンドログラムが書けます。
また、エネルギーの谷底(local minimum)になっているところの周り(basin)にどのような状態が集まっているのかも決定することができます。
こうして、すべての2^N個の状態にエネルギーの谷底(local minimum)かその周囲(basin)のラベルが付きます。すると、元の時系列が今そのEnergy Landscapeの中でどこにいるのかを定義することができ、このエネルギー地形を状態が動いていくという解釈をすることが可能となります。
公開したプログラム(Energy Landscape Analysis Toolkit: ELAT)
ダウンロードはこちらから
今回、この分析を簡単に利用してもらえるように時系列データを読み込むだけで全部自動的に出してくれるMATLABのプログラムコードを公開しました。ここではその使い方とできることについて紹介したいと思います。
準備
1.分析する時系列データを用意してください。現状、変数の数は20以下くらいでないとうまく分析できません。ファイルは数字だけからなるデータで各行が各変数の時系列になるようにします。つまり横(列)方向に時間が進んでいく向きで準備してください。連続値のデータの場合はELATが指定された閾値で二値化しますが、それが嫌な場合(データによってはもっと良い方法があるはずなので)はご自分で二値化した後のデータを準備します。
2.変数名リストのファイルを用意していただけると出力結果に反映されます。なくても動きます。
3.私のサイトからELATをダウンロードしていただき、適当なところに解凍してください。
ELATの使い方
1.MATLABを起動し、”StartProgram.m”を実行します。すると次のようなウィンドウが出ます。
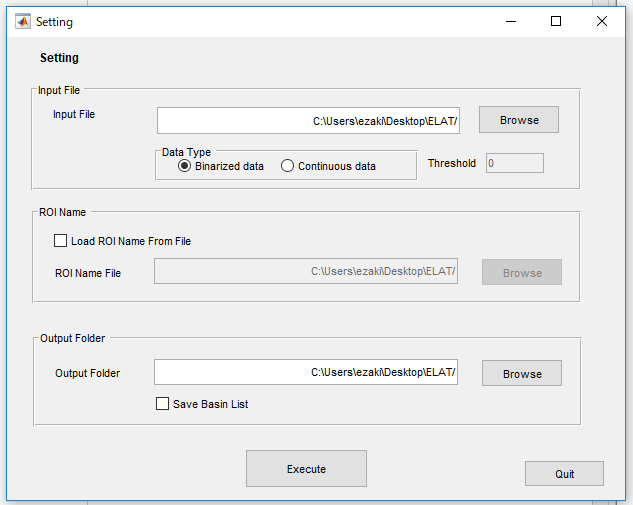
2.データファイルを読み込みます。テストデータとして"testdata.data"が入っているのでとりあえず動くか試してみたい方はそれを読み込んでください。
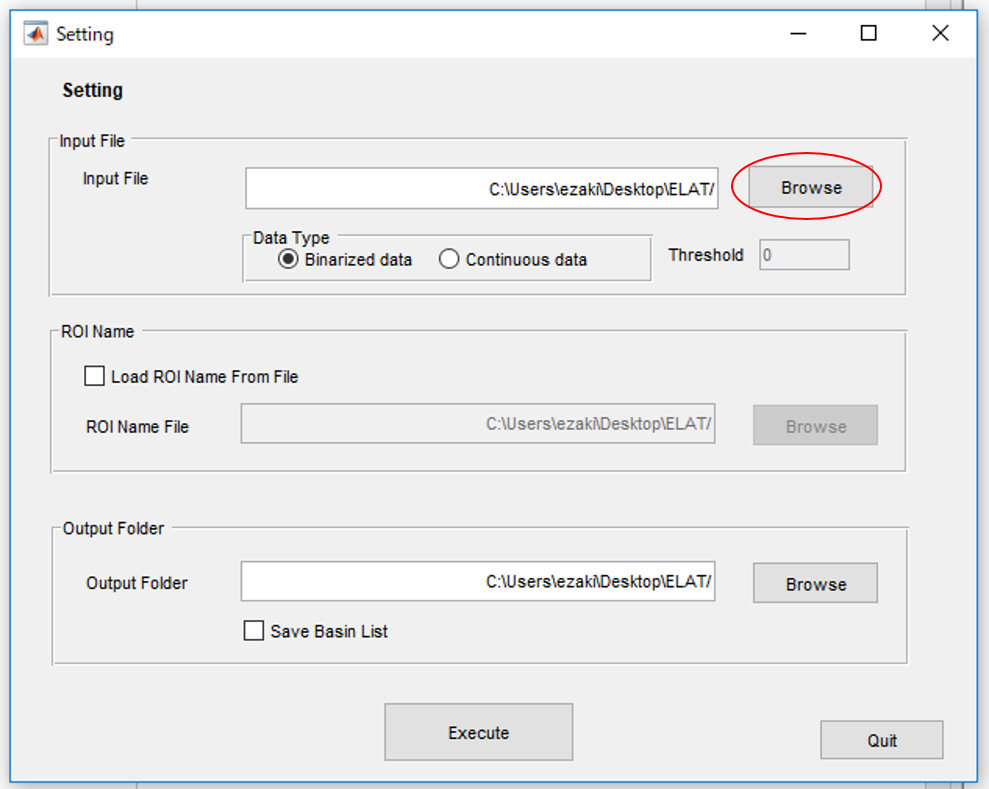
3.テストデータは既に二値化されているのでData typeは"Binarized data"を選択します。
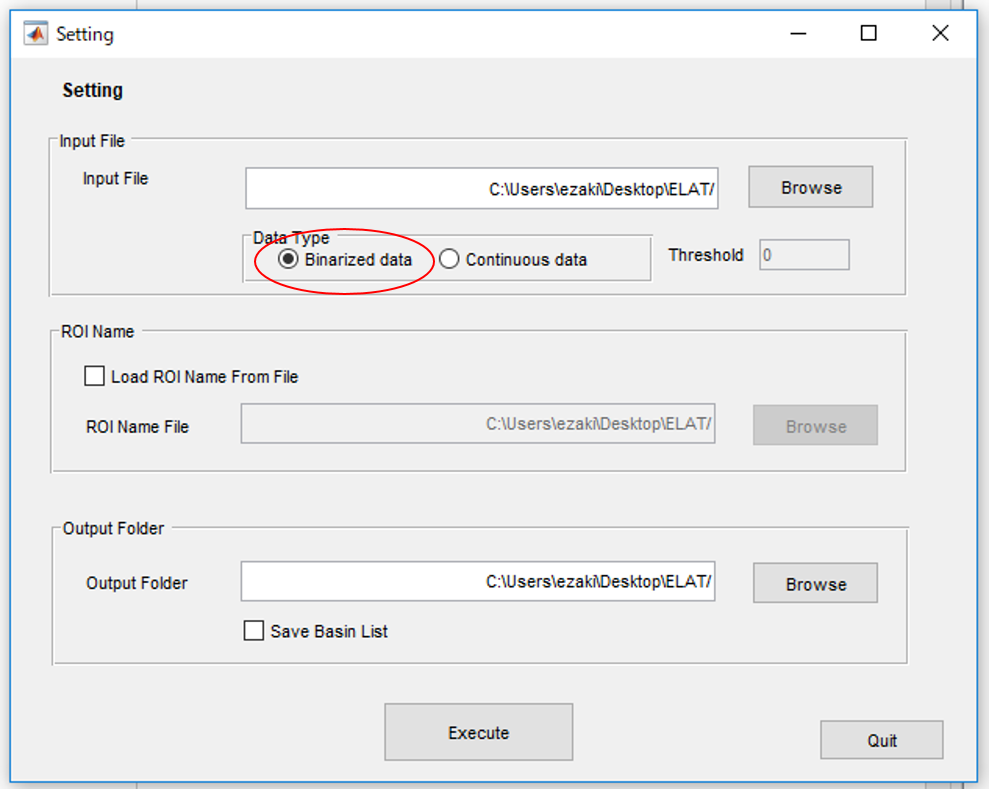
連続値のデータを読み込んだ場合は、"Continuous data"の方を選択します。この時Thresholdが選択できますが、特段の理由がなければデフォルトの0のままで良いと思います。尚、fMRIデータでgroup内の被験者をひとまとめにpoolしたデータの場合、二値化は被験者ごとにやったほうが良い(base lineの値が違ったらこまる)ので、先に別途二値化したものを用意することをお勧めします。
4.変数名(ここでは、脳の領域の名前)のリストが(あれば)読み込みます。ここではテストデータ"roiname.dat"を読み込みます。
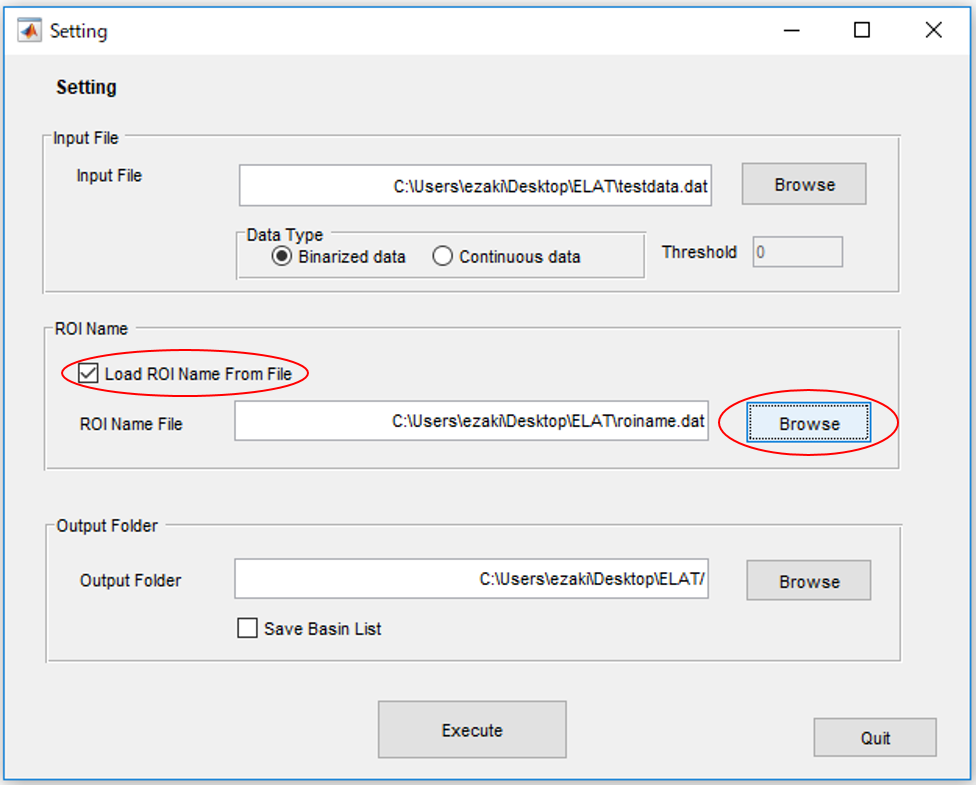
5.最後に結果が保存されるフォルダを指定します。後の分析のためにbasinの定義(どの状態がどのエネルギーの谷に属するか)も保存したい場合は"Save Basin List"にチェックを入れます。
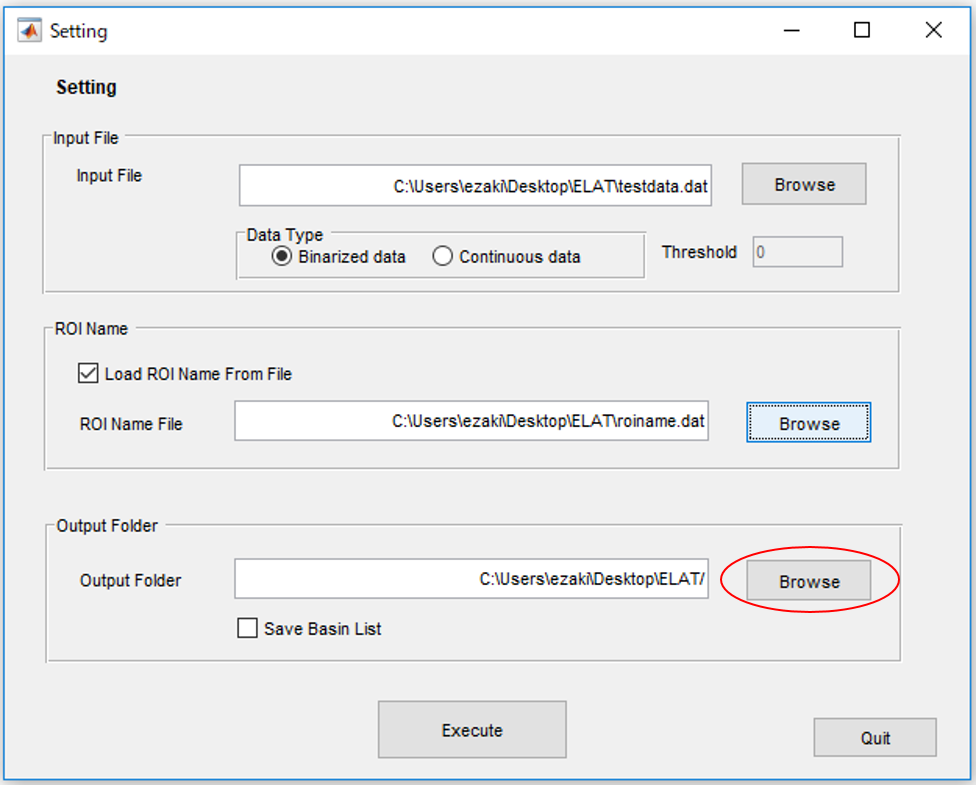
6.Executeを押します。
結果
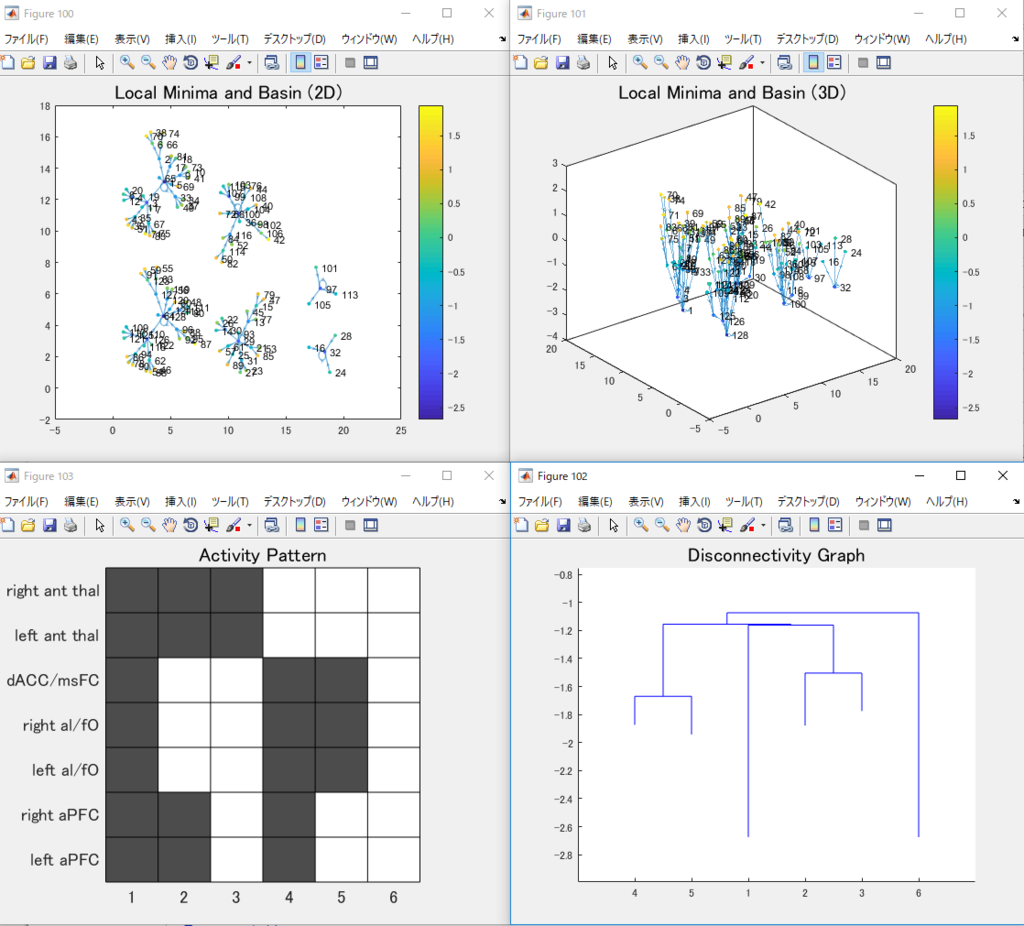
上段の二枚は2^N個の状態をlocal minimumとそのbasinに分類した絵です。
数字はそれを二進数表示にして、1 → +1, 0 → –1と読み替えたときに出てくるパターンに対応します。色と高さはエネルギーの値を表します。
下段の右はdisconnectivity graphでlocal minimumになっている状態の間をエネルギー地形の上で行き来するときにどれだけエネルギー差があるかをまとめたものです。横軸は状態(定義は下段左)で縦軸はエネルギーの値を表します。
この後は何をすればいいのか?
この分析では、状態空間を粗視化したものとエネルギー地形的な解釈を与えますが、それだけで分析が終了ということではなく、それを足掛かりにしてより詳細な分析を行います。問題の対象や設定によって異なると思いますが、例えば
1.disconnectivity graphの形が条件AとBで異なっているかをみる
2.あるlocal minimumの周りでの状態の滞在時間や遷移レートなどの指標に着目してデータを分析する
などが考えられます(具体例については論文 [1] のイントロで紹介した文献をご参照ください)。
その他注意事項
1.このコードを実行するためにはMATLABの2016bよりも新しいバージョンおよび Statistics and Machine Learning Toolboxが必要です。
2.時系列の変数の数ですが15より小さいくらいでないと動きません。ただ、ボルツマン分布を求める部分については数百まで増やしても動きます(が、データによってパフォーマンスはまちまちなようです)。
3.同梱されているmain.mで一通りの分析が行えますので、適宜ご利用ください。
4.理論的なことや技術の詳細に関しては論文 [1](OAなので誰でも読めます)に書いてありますのでご参照ください。
5.バグや質問等ありましたら江崎でご連絡ください。
[1] T. Ezaki, T. Watanabe, M. Ohzeki, and N. Masuda, "Energy landscape analysis of neuroimaging data", Phil. Trans. R. Soc. A 375, 20160287 (2017).
[2] T. Watanabe, N. Masuda, F. Megumi, R. Kanai, G. Rees, "Energy Landscape and dynamics of brain activity during human bistable perception", Nat. Commun. 5, 4765 (2014).
[3] T. Watanabe, S. Hirose, H. Wada, Y. Imai, T. Machida, I Shirouzu, Y. Miyashita, N. Masuda, "Energy Landscapes of resting-state brain networks", Front. Neuroinform. 8, 12 (2014).
新しい環境
四月からとあるプロジェクトの研究員として働くことになり、都内のとある国立研究所に異動となった。ようやく研究室の引っ越しや様々な手続きがひと段落して研究体制が整った。研究環境としては非常によく、かなり集中して研究に取り組めると思う。
以前書いていた論文は少々の紆余曲折ののち無事レビューに回り現在査読中となっている。良い知らせを待ちたい。
3月くらいからデータ分析に関する新しい研究を始めている。これはうまくはまれば相当なインパクトが出るような研究で、非常に楽しみである。一通りの(新しい)既存手法でできることに関しては何とかコードを実装でき、実際のデータに適用してみて結果がどうか、ということを見はじめたところである。とはいえ、まだ実装が正しくできているか不安な面もあり、現在は正しさをチェックしている段階である。
本日からかなり本腰で研究の作業が再開できた。共著者に質問を投げたり、一通りのコードを整理して足固めがだいぶ進んだ気がする。明日もこの調子で進めていきたい。